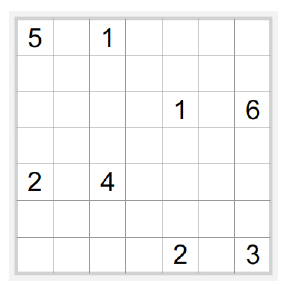
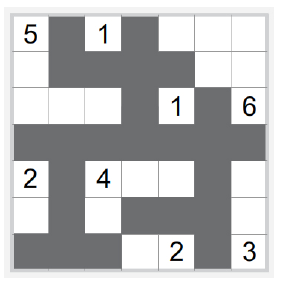
Your goal is to write a solver for Nurikabe, a binary determination puzzle. The puzzle is played on a grid, typically rectangular (with no standard size) containing empty and numbered cells. You must decide for each cell if it is white (land) or black (water), so that it satisfies the following constraints. An Island is a maximal connected region of white cells.

• The water areas must form one connected region. (All the black cells must be connected.)
• Each numbered cell must be part of an island.
• The number of cells in an island is equal to the number it contains.
• Every region (island) of white cells (land) must contain exactly one number.
• Two islands may not be connected.
• 2×2 blocks of black squares are not allowed.

Note that diagonal adjacency doesn't count as connectedness. You can assume there is always a unique solution for each puzzle.

Input 

There are multiple test cases in the input. The first line of each test case contains two numbers n , m (3n, m9) which are the dimensions of the puzzle, followed by n lines each one has m characters including `.' (indicating an empty cell) and 1-digit numbers. The last line of the input contains two zero numbers.

Output 

The output for each test case should show the solved puzzle. Show black (water) cells with `#'. Write an empty line in the output after each puzzle.

Sample Input 

3 4 
3... 
.... 
.4.. 
5 5 
2.5.. 
..... 
..... 
..... 
..4.3 
0 0

Sample Output 

3..# 
#### 
.4.. 

2#5.. 
.#.## 
##.#. 
.###. 
..4#3