along
with the states of the eight cells surrounding it. In the standard Game of Life,
a cell remains alive if it has two or three neighbours, and an empty cell
becomes alive if it has precisely three neighbours: otherwise, a cell
dies or stays empty. The figure below shows three generations of a
simple but surprisingly complex Conwayian structure called a glider:
0 1 2 3 4
....... ....... ....... ....... .......
....... ...A... ..AA... ..AA... .AAA...
..AAA.. ..AA... ..A.A.. .AA.... .A.....
..A.... ..A.A.. ..A.... ...A... ..A....
...A... ....... ....... ....... .......
....... ....... ....... ....... .......
As one can see, the entire structure has in fact moved one cell up and one
cell to the left after four turns. There are many other much more complex
structures in the Game of Life; it is even possible to build a (very, very slow)
Turing Machine on the grid, or simulate the Game of Life itself!
The ruleset for the original Game of Life can be described as
23/3; that is, a cell stays alive in turn n +
1 if it has two or three live neighbours in turn
n , and a dead cell turns
live if it has precisely three neighbours. There are many other ``Conway-like"
rulesets that can be described with the same notation. Note that a ruleset like
/234 (that is, all currently live cells die, but any dead cells with two,
three, or four neighbors come alive) is perfectly valid (and quite interesting);
rulesets with no ``birth values" are also valid but (unsurprisingly) dull. Your
goal is to simulate a number of these rules...at the same time on the same grid.
Because there is more than one ruleset running on the same grid, a number of
clarifications are required:
- Each cell can be occupied by at most one cell from one species (a ruleset
represented by a particular letter);
- Only cells of the same species count towards the state of the next turn
for that species;
- When there is a conflict as to the state of a cell in the next turn,
resolution is as follows:
- If one ruleset will place a live cell and all others leave the cell
dead, place a live cell of the ruleset that allows it;
- If more than one ruleset will place a live cell in that location, the
ruleset whose representation is first in alphabetical order wins (that is,
if species B and D would both have a live cell in a location, the cell
becomes a live cell with species B.)
- One can assume that the board is surrounded by an infinite number of dead
cells that cannot become alive.
After running a simulation for a given number of turns, you are to report the
maximum and minimum population of each species involved.
Input to this problem will begin with a line containing a single integer
n indicating the number
of simulations in the file. For each simulation, the first line contains three
integers X Y S
(1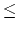 X, Y
X, Y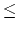 50;1
50;1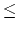 S
S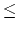 26) where X and Y represent the width and
height of the board and S
represents the number of different species represented
on the board. The next Y
lines are a textual representation of the board in turn
0, as shown above. The following S
lines are the definitions of the rulesets for each
species, given in the format described above. The last line of each data set is
an integer T representing
the number of turns to simulate. (For example, the figure above was a simulation
of 4 turns.)
26) where X and Y represent the width and
height of the board and S
represents the number of different species represented
on the board. The next Y
lines are a textual representation of the board in turn
0, as shown above. The following S
lines are the definitions of the rulesets for each
species, given in the format described above. The last line of each data set is
an integer T representing
the number of turns to simulate. (For example, the figure above was a simulation
of 4 turns.)
For each data set, first print `Simulation #N ' where N is the number of the data
set, starting at 1. Then print S
lines, each of the format `Species S : At most M live, at least L live.' where S is the letter representation
of the species (starting with A), M
is the maximum number of that species alive in any turn
of the simulation (including turn 0), and L
is the least number of that species alive in any turn of
the simulation (including turn 0).
Special Note: The below diagram shows the initial state plus the
four following states of the second sample input:
0 1 2 3 4
..A.. ..... ..A.. ..... ..A..
..A.. .AAA. ..A.. .AAA. ..A..
..A.. ..... ..A.. ..B.. ..A..
..... ..B.. .BBB. .B.B. .B.B.
.BBB. .BBB. .BBB. .B.B. .B.B.
Note that in turn 4 the A species takes over a cell that would have otherwise
stayed as a B.
2
7 6 1
.......
.......
..AAA..
..A....
...A...
.......
23/3
4
5 5 2
..A..
..A..
..A..
.....
.BBB.
23/3
123/36
4
Simulation #1
Species A: At most 5 live, at least 5 live.
Simulation #2
Species A: At most 3 live, at least 3 live.
Species B: At most 6 live, at least 3 live.
![]() X, Y
X, Y![]() 50;1
50;1![]() S
S![]() 26)
26)