Janken, also known by the name rock paper scissors, is a popular Japanese childrens' game. In the grand tradition of game development, one company has decided to put a strategic twist on a classic title. The resulting war ``simulation," Janken Tactics, is in development as we speak. You have been hired onto the team as a programmer, and put to work on the move validation code.

Janken Tactics takes place on a map represented by a hex-hex grid with five cells on each side. Each cell on the grid has a certain terrain type, which helps or hinders movement through the cell. Normally, moving into an adjacent cell costs one movement point, but the terrain on that cell may cause it to cost more:

• Moving into a Field costs no extra movement points (one total);
• Moving into the Woods costs one extra movement point (two total);
• Moving into the Hills costs two extra movement points (three total);
• Moving into the Mountains costs three extra movement points (four total);
• and no units may move into Underwater cells. (They will not start in an underwater cell either.)

The layout and coordinate system for the hexagonal grid is as follows:

 
      4 5 6 7 8 9
     3 \ \ \ \ \ \                
    2 \ \ * * * * * -- A
   1 \ \ * * * * * * -- B
    \ \ * * * * * * * -- C
     \ * * * * * * * * -- D
      * * * * * * * * * -- E
       * * * * * * * * -- F
        * * * * * * * -- G
         * * * * * * -- H
          * * * * * -- I

As one might expect of a game based on Janken, there are three unit types: the Guardian (rock), the Mage (paper), and the Swordsman (scissors). Units also have 10 movement points that they can expend per move. And, as in Janken, the units each have their strengths and weaknesses:

• Guardians can defeat Swordsmen but are defeated by Mages;
• Mages can defeat Guardians but are defeated by Swordsmen;
• and Swordsmen can defeat Mages but are defeated by Guardians.

You are not working on the combat code for Janken Tactics, but the strengths and weaknesses are important for another reason: during a move, a unit cannot pass over an enemy unit, NOR can they pass within one cell of an enemy unit that is strong against them (that is, a Guardian cannot pass within one cell of a Mage, a Mage cannot pass within one cell of a Swordsman, and a Swordsman cannot pass within one cell of a Guardian). They may, however, end a move in a cell adjacent to (but not the same as) any enemy unit, and may pass through cells occupied by allied units of all types. The destination cell must not have any unit (allied or enemy) inside. There will never be more than one unit in a cell between moves.

Your goal is to determine whether a given unit can execute a certain move, and if so how many movement points are left over after the move. The code should maximize the number of movement points left at the end of the move, so that the unit has more choices during any potential combat that may occur. Invalid moves may occur if:

• the starting cell has no occupying unit;
• the destination cell is already occupied;
• moving to the destination cell costs too many movement points;
• or the destination cell is impossible to reach without passing over Underwater cells, enemy units, or passing next to enemy units which are strong against the moving unit.

You will be processing a sequence of moves, so if a move is invalid, leave the unit which attempted to move (if any) in its starting location. Every move in a particular data set takes place one after the other, so do not reset the grid to its initial condition after each move.

Input 

Input to this problem will begin with a line containing a single integer n indicating the number of data sets. For each data set, the next six lines are a representation of the hex-hex grid's terrain, with F representing fields, W representing woods, H representing hills, M representing mountains, and U representing underwater cells.

The next line of each data set will consist of two integers M P (1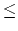M, P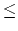10) representing the number of units on each side of the battle. Following that are M lines with two values T L , where T is the type of unit (G for Guardian, M for Mage, S for Swordsman) and L is the starting location for that unit represented as described above. The P lines following that are a similar representation for the second side.

The next line of each data set consists of an integer V (1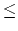V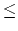100) representing the number of moves to test. The next V lines contain two values S E , where S and E are coordinates in the proper format describing the starting cell (and therefore unit) and attempted ending cell for that move. Note that moves may involve either of the sides.

Output 

For each data set, first print `Game #X ' where X is the number of the data set, starting with 1. For each move in each data set, print `Move #N (S -> E ): Successful (M points left)' if the move was successful, or `Move #N (S -> E ): Unsuccessful' if the move was unsuccessful. N is the move number, starting at 1; S is the starting coordinate and E the destination coordinate, in the representation described above; M is the number of movement points left at the end of the move.

Sample Input 

 
1
    U U U W W
   U F F F F W
  W F H H H F W
 W F H F F H F W
W F H F F F F F W
 W F H F F H H H
  W F H M M M M
   W F F F F F
    W W W W W
3 3
G E5
M D5
S F4
G F8
M A8
S C4
2
E5 E9
D5 F8

Sample Output 

 
Game #1
Move #1 (E5 -> E9): Successful (5 points left)
Move #2 (D5 -> F8): Unsuccessful